Végtelen találmányok
Szöveg: Magyar Péter
Gondolatban, majd rajzban is megfoganva, mindketten negyvenes éveikben vannak. Egyikük, melyet Cubicumnak kereszteltem el, kocka-felületek megcsonkított sarkainál összekapcsolt terek végtelenségig folytatható sorozata, építészeti alkalmazását szépen mutatja az Oro Kiadónál 2019-ben megjelent könyvem címlapja. Itt tisztán látszik, hogy csatlakoztatásra fel nem használt, úgynevezett szabad vegyértékek jól szolgálják az épület múzeumi funkcióját, amikor becsalogatják a velencei környezet látványát a belül kialakított anyag kiegészítéseként.
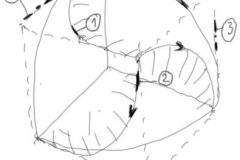
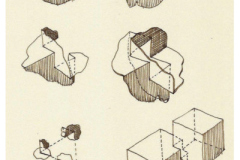
Egyelőre még közvetlen építészeti alkalmazhatóságot nem ismerek fel a második, most 3D nyomtatással szó szerint megtestesített, eddig még – úgy gondolom – nem ismert geometriai konfigurációnál, habár annak az elvnek az igazolását kutattam születése idején, hogy a térfolyamatosság feltétele a felületfolytonosság jelenléte. Ez utóbbi, a felület, azzal a speciális képességgel bír, hogy egyszerre tudja elemezni és leírni a teret és a nem-teret, azaz a tömör anyagot és a végtelen űrt! Egy több rajzból álló „kérdezősködés” két csoportja már előre jelezte azoknak a testeknek a létezhetőségét, melyeket most – a nyomtatás következtében – fizikai valóságukban láthatunk és tapinthatunk.
Itt, ha szabad, egy kis kitérést szeretnék tenni, és pár szóval kifejteni, hogy az általam (is) gyakorolt, a gondolatokat szabadkézi rajzokkal megörökítő tervezői metódus – egyéb funkciói mellett – az építészeti alapkutatás egyik módszereként is értelmezhető, így szinte természetes, hogy néha az alapgeometria kincsestára – minden ilyen előzetes szándék nélkül – egy új elemmel bővülhet.
Mivel a gömb középpontján keresztül metszett kör íveinek a negyede, és egy zéró sugarú tórusz tizenhatoda, és ezek sokszorosai képezik mindegyiket ennek a három tagból álló geometriai családnak, ezért a két alapgeometria angol neveit kombinálva, Spherusnak neveztem el őket (Spherus 1, Spherus 2a és Spherus 2b módon jelölve a formai variációkat). Mindhárom formáció egy gömb és az őt érintő kockafelület közötti „légtérben helyezkedik el, és a több negyedkör adott tengely körüli elfordításával képezik a „tórusz-sziromnak” elnevezett, két irányban görbült felületeket, melyeknek többszörösei egy zárt testet képeznek, három megjelenítési formában. Ezt a szűkös „szókincset” már a rajzok is megjósolták, de igazából csak a látás és a tapintás együttes érzékelése képes teljes bonyolultságának kifejezni e testek szépségét. Nagy köszönet illeti a Limes modellkészítő céget, ahol a háromdimenziós nyomtatás segítségével ezek az új, eddig nem látott felületbravúrok szó szerint megfoghatóvá válhattak.