Szöveg: Sugár Péter

Amikor épületek alaprajzait tervezzük, egy leképezési rendszert alkalmazunk, és ha hozzánézzük a metszeteket és a homlokzatokat, és ezek alapján próbáljuk meg a teret elképzelni, akkor sem tudjuk ezt maradéktalanul megtenni. Ezért is alkalmaznak az építészek háromdimenziós maketteket a terek megkomponálása közben. Mégis, gyakran van olyan érzésünk, hogy egy alaprajznak is van valamiféle önmagáért-valósága. Valami mást mond el az épületről, egy olyan dimenziót, „láthatatlan” valóságot mutat, fed fel, amelyet az épület térbeli megtapasztalásakor nem feltétlenül érzékelünk. Ez a valóság „a terv”, a generáló szándék, akarat, ha úgy tetszik, a mögöttes filozófia, aminek a rajz csak grafikus leképezése. A geometriai logika és a térbeli valóság összefüggenek; mindkettő mögött ott van az elvont mértani struktúra.

Alaprajzi kompozíció és világkép

Az építészetben a szerkesztett struktúrával rendelkező kompozícióknak a felületeket borító díszítés, az ornamentika az egyik jellegzetes megjelenési formája. A másik az épületek alaprajzaiban megnyilvánuló kompozíciós rend.1 Mindkét formáció a geometria szerkesztési rendszerein alapszik – és a geometrikus ornamentikának is ez az alapja –, ezért mindkét megnyilvánulást ornamentikának tekintem – az egyszerűség kedvéért és a jelen tanulmányban kifejtendő koncepció értelmében. Kérdés, hogy egy ilyen megfogalmazásból mi következik, milyen irányba visz minket egy ilyen kijelentés? Hiszen az ornamentika kifejezés „foglalt” – díszítést, díszítőművészetet értenek alatta. Talán messzebb és tovább juthatunk, ha abból indulunk ki, hogy a szerkesztett rendszerek mögött lévő struktúra – művészetről lévén szó – összefügg a korszak világképével. Szentkirályi Zoltán egy tanulmányából idézve: „A kompozíció zárt egységében tekintett művészi formát objektíve a kor természettudományi megalapozottságú világképe határozza meg”.2 Az ornamentika mintázataiban és a „klasszikus” építészetben ez az alap matematikai-geometriai és a szimmetriarendszereket jelenti. (A későbbiekben látni fogjuk, hogy ahogy haladunk az építészet történetében a kezdetektől az időben előre, és eljutunk egészen a 20. századig, az alaprajzokban a hagyományos tengelyes és centrális szimmetriák mellett megjelennek a természettudomány által feltárt összetettebb és bonyolultabb szerkesztési rendszerek is.)

Tektonikus és atektonikus ornamentika

Az építészetben az ornamentikának kétféle jelleget tulajdonítok: az egyiket tektonikus, a másikat atektonikus ornamentikának tekintem. A tektonikus a fizika törvényszerűségeinek, a nehézségi erőnek engedelmeskedik, és az anyag, az építőelemek térbeli elhelyezkedése jellemzi. Az atektonikus jellemzően a síkban jelenik meg, és a síkgeometria törvényszerűségeit követi (izometrikus transzformációk, szimmetriacsoportok). Vannak persze átmenetek, keveredések, például ahol egy kristályszerkezeti formáció épület-méretben kilép a térbe, és egyszerre mindkét jellegnek megfelel. Az épületek alaprajzaiban megnyilvánuló ornamentalitásnak az a sajátossága, hogy egy síkgeometrikus mintázat a térben úgy válik háromdimenzióssá, hogy közben megőrzi atektonikus jellegét.3 A továbbiakban a síkbeli absztrakt-geometrikus mintázatok struktúrájának az építészettel való kapcsolatát vizsgálom.

Ornamentika síkban és térben

Antoine Picon elmélete szerint az ornamentika leválasztható az építészet „csontvázáról”, és a díszítés hiánya a művészi dimenzióktól fosztja meg az architektúrát.4 Ez a leválaszthatóság a síkbeli és a térbeli megjelenés közti viszonyt is érinti. Az ornamentika történetében fordulatot hozott a 19. század második felében Owen Jones alapműve, a The Grammar of Ornament.5 A gyűjtemény a világ minden részéből összegyűjtött díszítőmotívumokat korok és kultúrák szerint rendszerezte. Az építészeti tagozatokról, térbeli elemekről a mintázatokat (ornamenseket és ornamentumokat) leválasztotta, és a síkban kiterítette.6 Ezzel a módszerrel tulajdonképpen megfordította, visszafejtette az alkotási folyamatot, amely eredetileg a síkban történő szerkesztéssel indult, majd az ornamens, ornamentum vagy a síkban maradt, vagy az épület valamely tagozatára került, felvéve annak térbeli alakját.7 Eszerint tehát a síkban szerkesztett ornamensek is meg tudnak jelenni három dimenzióban, anélkül, hogy ténylegesen tektonikus szerepük lenne, hiszen ebben a megjelenési formájukban az építészeti tagozatok díszítésére, hangsúlyozására szolgálnak. Jones műve megnyitotta a sorát azoknak a mintakönyveknek, amelyek az építészeti ornamentikára mint absztrakt vagy stilizált motívumoknak a síkban történő sokszorozására tekintettek.

Ornamentika az alaprajzokban

Visszatérve a kezdeti gondolathoz, azt állítom tehát, hogy a síkban szerkesztett geometrikus ornamentika mintázatai és az épületek alaprajzainak (vagyis térszervezésének) a mintázatai között mély strukturális kapcsolatok, analógiák és megfelelések vannak; az alaprajzok bizonyos értelemben ornamentikáknak is tekinthetők – nem tektonikus jellegűeknek, hanem atektonikusnak (szóhasználatom szerint „apollóninak”8). Ez utóbbi jelzővel arra is szeretnék utalni, hogy az alaprajzok mintázatai „égi mintázatok”, vagyis szellemi-filozófiai konstrukciókkal (vallási vagy természettudományos világképpel) állnak összefüggésben. Természetesen a funkció, az adott beépítési körülmények, a telek morfológiája befolyásolhatja és módosíthatja a „tiszta” szellemi konstrukciót, a geometriát. Sőt, a morfológiának való megfelelés, maga az organikus szerkesztés is lehet a szellemi konstrukció alapja.
A mély strukturális megfelelést az alaprajzok és az ornamentika mintázatai között a geometria törvényszerűségei, a szerkesztő rendszerek azonossága vagy hasonlósága adja. A geometrikus ornamentika egyik legfontosabb módszere az elemek változtatás nélküli (izometrikus) ismétlése, amely a természetben működő sokasodás, szaporodás alapelvét követi.9
Az ornamentika-szerkesztések geometrikus szabályai nemcsak a díszítőrendszerek megalkotására voltak jók. Az építészek ugyanezeket a geometriai módszereket használták az egyszerű vagy összetett alaprajzok és térbeli rendszerek tervezésekor. Körzőkkel és vonalzókkal (majd CAD-programokkal) szerkesztettek, alapelemeket sokszoroztak, tulajdonképpen alaprajzi és térbeli ornamentikákat hoztak létre. Sőt, a modernizmus alatt sem tűnt el az ornamentika, csak „visszahúzódott” az alaprajzi-térbeli struktúrákba.
Az ókortól a középkoron át fennmaradt jelek, kódexek, feljegyzések tanúságai szerint az építészek, pallérok tevékenységében nem vált külön egymástól az alaprajzi-metszeti és az ornamentikai rendszerek szerkesztésének tudása és a mérnöki-technikai tudás. A matematikai ismeretek mellett feltehetőleg az ornamensek és ornamentumok szerkesztésének a megtanulása révén tehettek szert arra a geometriai tudásra, amely alkalmassá tette őket az egész épület konstrukciójának a megalkotására. Tudjuk, hogy már az ókorban is komoly matematikai (geometriai) tudás jellemezte az építészeket, Iktinosz és Kallikratész a Parthenon, vagy tralleszi Antemiosz és milétoszi Izidórosz, a Hagia Sophia építészei kiemelkedő matematikai tudással rendelkeztek.10

Formációk: tengelyes és centrális szimmetriák

Némi leegyszerűsítéssel azt állíthatjuk, hogy a „történeti építészetben”, elsősorban a 19. század végéig a reprezentatív szakrális és világi építmények alaprajzait a tengelyes és/vagy centrális szimmetriára épülő szerkesztések határozták meg.11 A 20. században az aszimmetria hangsúlyozása miatt az eltolásos szimmetriákkal kombinálták a térszervező megoldásokat, majd – még mindig maradva a geometria szimmetria-rendszereinél – megjelentek a három dimenzióban történő szerkesztések is.
A szimmetrikus geometriai rendszerekben három sokszorozó alapműveletről beszélhetünk: tükrözésről, elforgatásról és eltolásról. Az összefoglalóan szimmetriacsoportoknak nevezett izometrikus transzformációknál a tükrözés és az elforgatás a pontcsoport-szimmetriáknál, az egy irányban történő eltolások a frízcsoportoknál, a kétirányú eltolásos szerkesztések az ún. tapétacsoportoknál jelennek meg. Az utóbbi csoport formációi magukban foglalják az előző csoportokéit, és a matematikusok szerint a síkban 17-féle, a térben 230-féle transzformációjuk létezik.12 Már az ókori egyiptomi sírkamrák díszítőmotívumait vizsgálva már kimutatták mind a 17-féle formációt, de ugyanez vonatkozik például a magyar népművészet archaikus gyökereket őrző díszítőművészetére is.13
A következőkben néhány kiragadott példával fogom illusztrálni felvázolt gondolatmenetemet. Elsőként vizsgáljuk meg a tengelyes és tükrözéses szimmetrikus alaprajzi formációkat!
Az elforgatás és a tengelyes tükrözés szerkesztő műveleteit az ornamensek (díszítőmotívumok) szerkesztésénél tapasztalhatjuk a leggyakrabban mint a stilizáció, dekompozíció absztrakciós eszközeit.14 A legáltalánosabban használtak a legegyszerűbb geometriai alapelemek, a négyzet és a kör, illetve a háromszög és a szabályos sokszögek, amelyeknek mind szimbolikus jelentésük is van.15 De az első városok, majd a reneszánsz ideális városai, a korai szakrális építmények, az első várak alaprajzainál is találkozhatunk a geometria alapelemeivel és ezek kombinációival, amelyek befejezett, önálló voltukban építészeti ornamenseknek is tekinthetők.

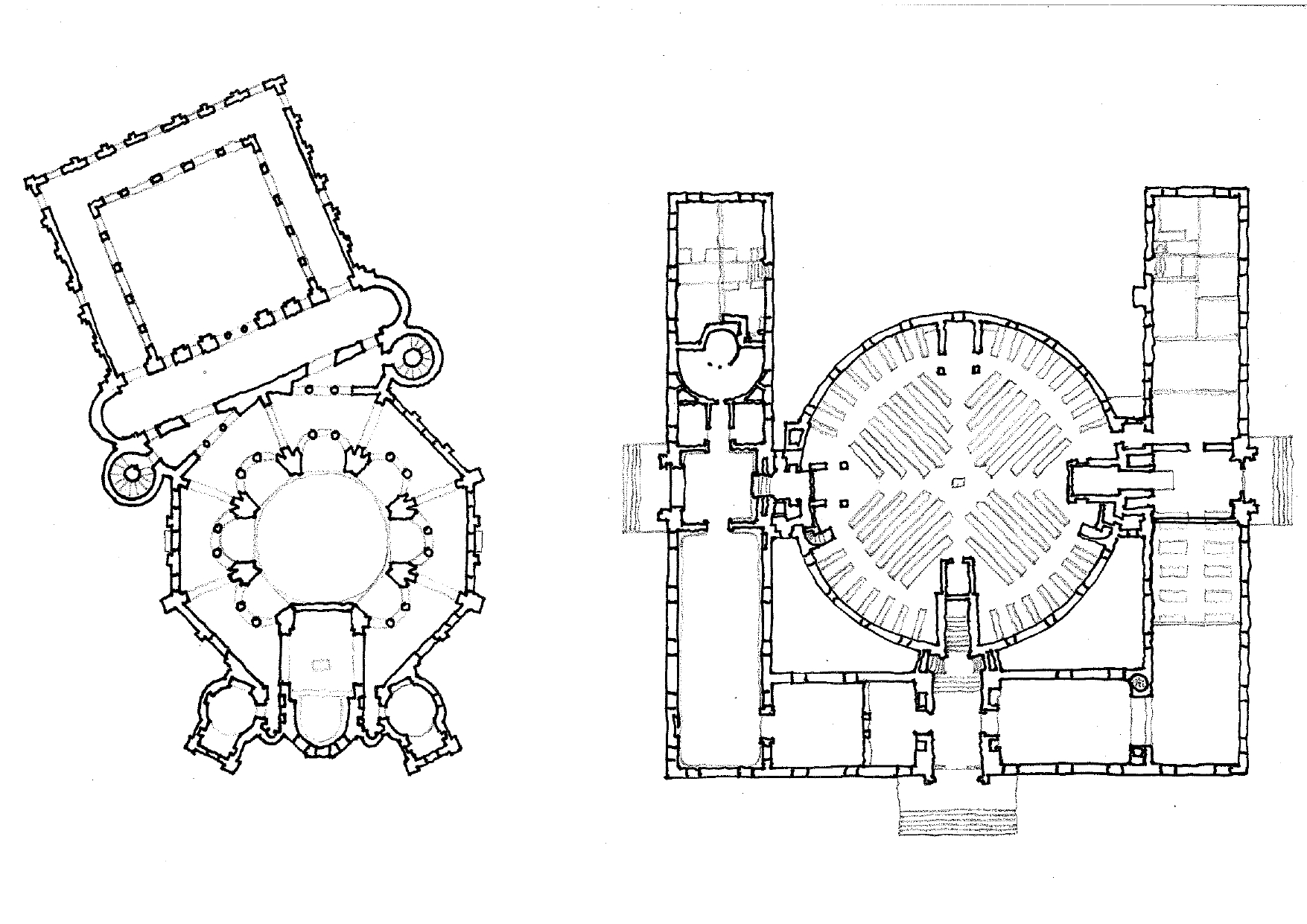
Balra: Ravennai San Vitale, 526–547; jobbra: Erik Gunnar Asplund: Stockholmi Könyvtár, 1922–1923

A ravennai San Vitale alaprajza a centrális és a többszörös tengelyes tükrözés megragadóan szép példája. Az épületről az is leolvasható, hogy a belső térhatás és a szerkesztés szakralitása volt meghatározó, a külső megjelenés inkább csak következmény. Gunnar Asplund stockholmi könyvtárépületének az alaprajzi kompozíciója kompakt szimmetrikus egységekből épül fel, a városképben emblematikus és archetipikus tömegformákat felmutatva.
A további példákban láthatjuk, hogy ezeket az egyszerűbb térelemeket ornamensekként sokszorozva hoztak létre összetettebb alaprajzi formációkat. 1756-ban Giambattista Piranesi elvégezte az Augustus-korabeli római Mars-mező reprezentatív császárkori középületeinek rekonstrukcióját. A patchwork-szerűen egymáshoz illesztett alaprajzok kollázsa a centrális és tengelyes tükrözéssel előállított formációk rendkívüli változatosságát és gazdagságát mutatja.
A 20. század ikonikus építésze, Louis Kahn philadelphiai irodájában az íróasztala fölött ott függött Piranesi Mars-mező rekonstrukciójának felnagyított képe. Piranesi antikizáló világa hasonlóan kreatív, tengelyesen és centrálisan szimmetrikus és monumentális alaprajzok megalkotására ihlette a 20. századi mestert (lásd a bangladesi parlament alaprajzát). Frank Lloyd Wright és Le Corbusier gyakran és igen kreatívan alkalmazták ezeket az ornamentika-szerkesztésekben tanult geometriai ismereteiket. Wright Price toronyház-terve, vagy Corbusier hárommillió ember számára tervezett utópikus városelképzelése (Ville Contemporaine) az elforgatással, tükrözéssel kombinált szerkesztések mintapéldái.

Formációk: eltolásos szimmetriák

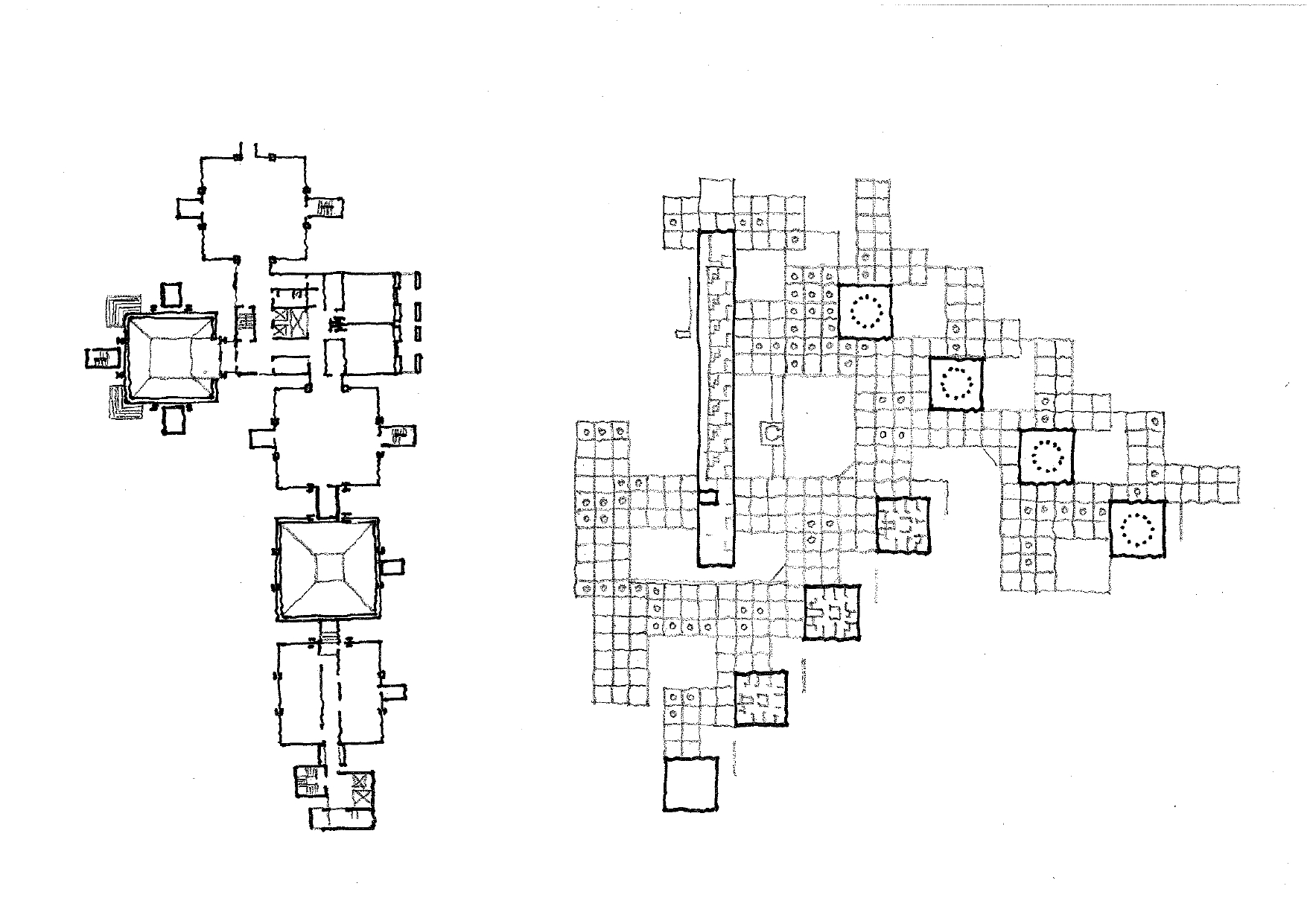
Balra: Orvosi kutatólaboratórium, Philadelphia, 1957–1964, építész: Louis I. Kahn; jobbra: Árvaház, Amszterdam, 1960, építész: Aldo van Eyck

A díszítőművészetben az egyirányú eltolással az úgynevezett szalagmintáknál találkozhatunk, amelyek az építészeti tagozatoknál, a leggyakrabban párkányok, lizénák, kapuzatok, nyíláskeretezések formájában jelennek meg. Az egyirányú eltolás eklatáns példáit láthatjuk az ókeresztény templomok, vagy a román kori és gótikus templomok, székesegyházak alaprajzait vizsgálva. Az ókeresztény bazilikáknál egy pillérköz a fölötte lévő falmezővel és a rajta lévő alakos mozaik-ábrázolással tekinthető alapelemnek, amelynek a szentély felé történő eltolásos ismétlése a kompozíció alapja. A román vagy gótikus templomoknál az ismétlés alapjául szolgáló „ornamens” már összetettebb térbeli elem: egy boltozattal fedett mező, amelynek eltolása, majd ennek a szentélyben való elforgatása és az egész alaprajz megtükrözése révén alakul ki a templom sajátos térrendszere. A legtöbbször ez a boltmező a metrum, az egész térrendszer alapmodulja (a tartóoszlopaival és a bordáival); a főhajó és a templom egyéb, alaprajzi és magassági méreteit is ennek az alapmodulnak a többszöröseként határozták meg. Az egyirányú eltolás számtalan példájával találkozhatunk a modern, illetve a kortárs építészetben is. Ennek az egyszerű szerkesztésnek szép példája Louis Kahn Medical Research kutatóépülete, vagy pl. a TEd’A Arquitectes családi villa terve (House Barbel Tobias). A kétirányú eltolás leglátványosabb példáit az iszlám ornamentikában láthatjuk (a legtöbbször négyzet alakba foglalt elemek sokszorozásával, de előfordul a három- vagy hatszögbe foglalt formációk sokszorozása is). Ennek a szerkesztésnek az alaprajzi megfelelői például a mecseteknél jelennek meg (pl. a córdobai nagymecset alaprajza).
A 20. század nagy mesterei gyakorta alkalmazták ezt a sokszorozó szerkesztést. Louis Kahn ahmedabadi egyetemi épületegyüttesének a kétirányú eltolásos szerkesztések adják az alapját. Az ornamentális jellegű szerkesztettség a hatvanas évek strukturalizmusában teljesedett ki, az alaprajzok – a térszervezés – koherens mintázataiban. A strukturalizmusnál egyértelműen a rács (grid) volt a működő szerkesztési módszer (Herman Hertzberger: Central Beheer, Aldo van Eyck: amszterdami árvaház). De más 20. századi mestereknél (Ricardo Bofill, Hans Scharoun) is találkozhatunk ezekkel a szerkesztésekkel. Louis Kahn philadelphiai laborépületét azért is emeltem ki, mert az egyirányú eltolással ornamensként sokszorozott alapegység (egy függőleges pilonra szerkesztett négy irányban konzolos, sarkain nyitott térelem) az alapja Hertzberger Central Beheer kompozíciójának, de itt az elemek két irányban, sőt három dimenzióban vannak eltolva. Kortárs építészeti példa: a chilei Pezo von Ehrlichshausen építésziroda által tervezett Luna House sajátos keveréke a múzeumnak, a lakóháznak és valamiféle szakrális képződménynek. Leginkább az iszlám építészet hatását érezhetjük, a rács-alapmodulra épített szerkesztés miatt.
Az összetettebb alaprajzi rendszereknél az előző, tükrözéses vagy elforgatásos szerkesztéseket kombinálták az egyirányú, vagy a kétirányú eltolásokkal (Hagia Sophia, périgueux-i Saint-Front székesegyház, Aldo van Eyck hágai Pastoor Van Ars római katolikus temploma).

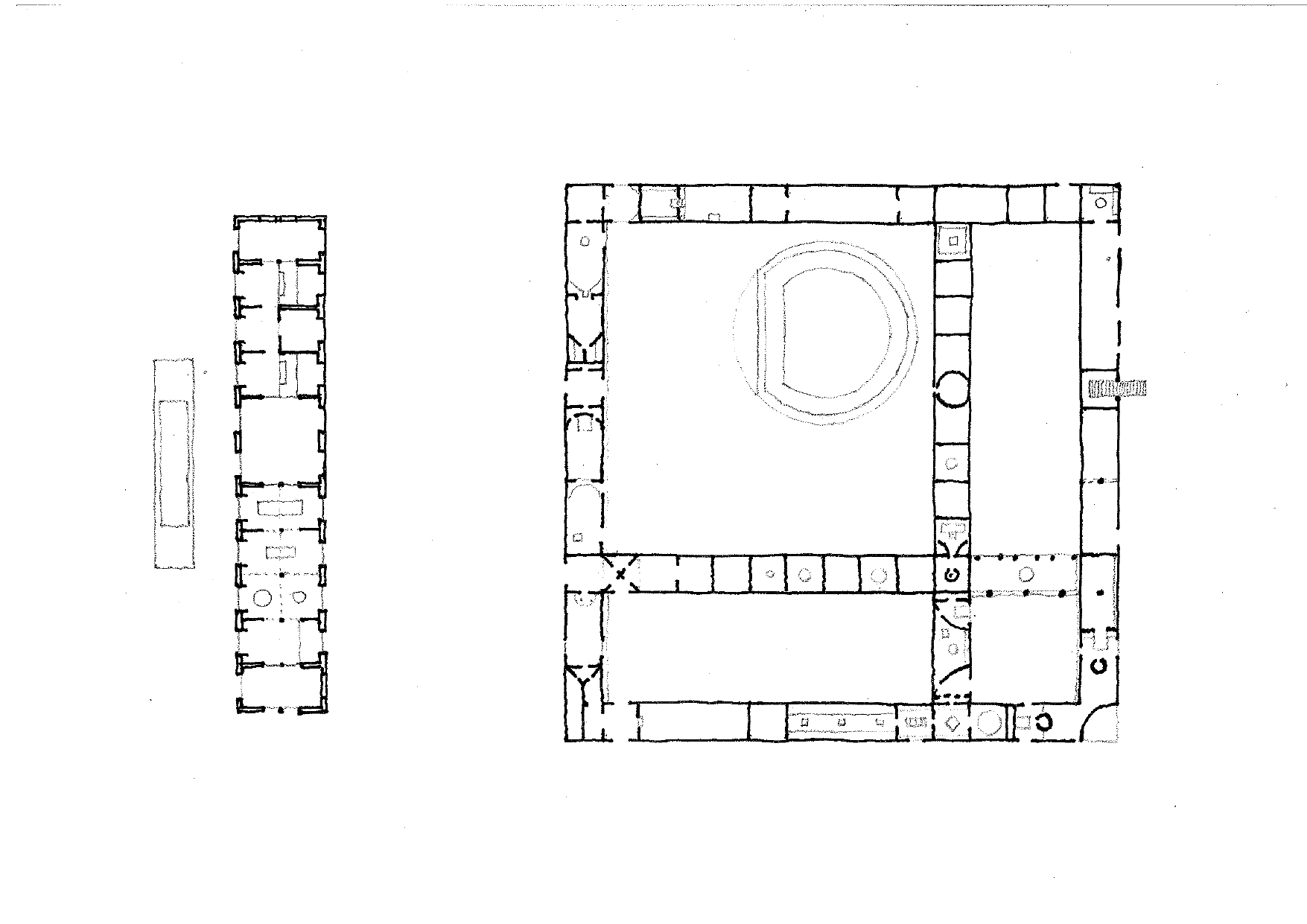
Balra: TE’dA Arquitectes: Barbel és Tobias háza, Mallorca, 2016–2018; jobbra: Pezo von Ellrichshausen: Luna House, Santa Lucia Alto, 2023;

Formációk: növényi szerkezetek, mitokondriumok, kristályszerkezetek, a véletlen mintázatai, káosz-fraktálok

A felvilágosodás korában az építészeti akadémiák létrehozásakor a geometriai képzés fontos része volt a botanika és az ásványok térbeli rendszereinek oktatása. 1928-ban jelent meg a botanikus és fotós Karl Blossfeldt Die Kunstformen der Natur című képgyűjteménye, amely növények virágzatainak, terméseinek mikroszkopikus felnagyításával megújította a természetről alkotott képzeteinket. A japán metabolisták előszeretettel alkalmazták utópikus alaprajzi/térbeli vízióiknál a növényi struktúrák formációit, de megvalósult épületekként a század közepén a növényi metabolizmusok struktúráit követték. Kenzo Tange 1966-os Yamanashi Broadcasting and Press Centre rádió és televízió székház épületénél a függőleges közlekedők és strangok (a metabolizmusok) alkotják a monolitikus teherhordó szerkezeteket, amelyek a födém és a helyiségek dobozait hordozzák. A rendszer 35 évvel később Toyo Ito Sendai Mediatheque (könyvtár, galéria, színház) épületénél köszön vissza megújult formában. A spanyol Mansilla + Tuñón építészpáros szinte minden, a természettudományok által „fölkínált” mintázatot megvalósított alaprajzban/térben. A mellékelt példa a 2011-ben a spanyol Lalinban épült városházájuk, amely a „növényi” mintázatokat valósítja meg térben.

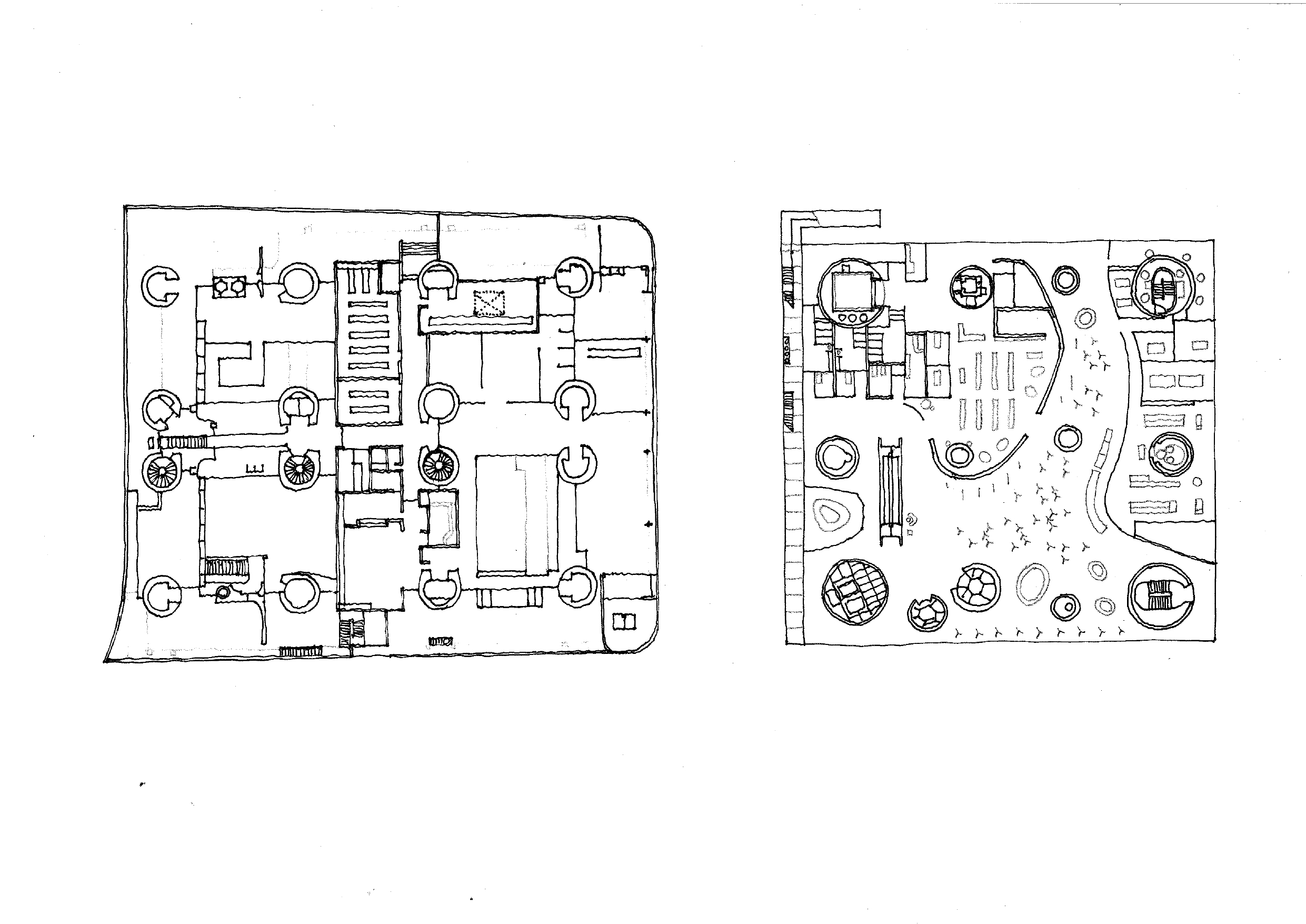
Balra: Kenzo Tange: Média- és sajtóközpont, Kofu, 1966; jobbra: Toyo Ito: Médiaközpont, Sendai, 2001

A kristályformációk komoly karriert futottak be a 20. század építészetében. Már Bruno Tautnál találkozunk velük, de a szilárd testek kristályszerkezetének – krisztallográfia – mintázatait háromdimenziós formációkként a strukturalista irányzat képviselői alkalmazták a legkonzekvensebben. Egyes építészek a hatvanas években kísérletképpen meg is tudtak valósítani bravúros térbeli formációkat. Zwi Hecker nagyobb léptékben jeruzsálemi lakótömbjeiben építette meg bonyolult kristály formájú mintázatait (Ramot Housing II. ütem, Jeruzsálem, 1979–1983). Piet Blom, a holland strukturalizmus képviselőjének rotterdami kockaházai és helmondi kulturális központja jellegzetes városképi elemekké váltak: a kristályos formájú elemek között létrehozott passzázsok figyelemre méltó városépítészeti eredményeket mutatnak. A kortárs japán építészetben ennek az építészeti hagyománynak a továbbvitelét láthatjuk például Toyo Ito és Hiroshi Nakamura épületeinél.

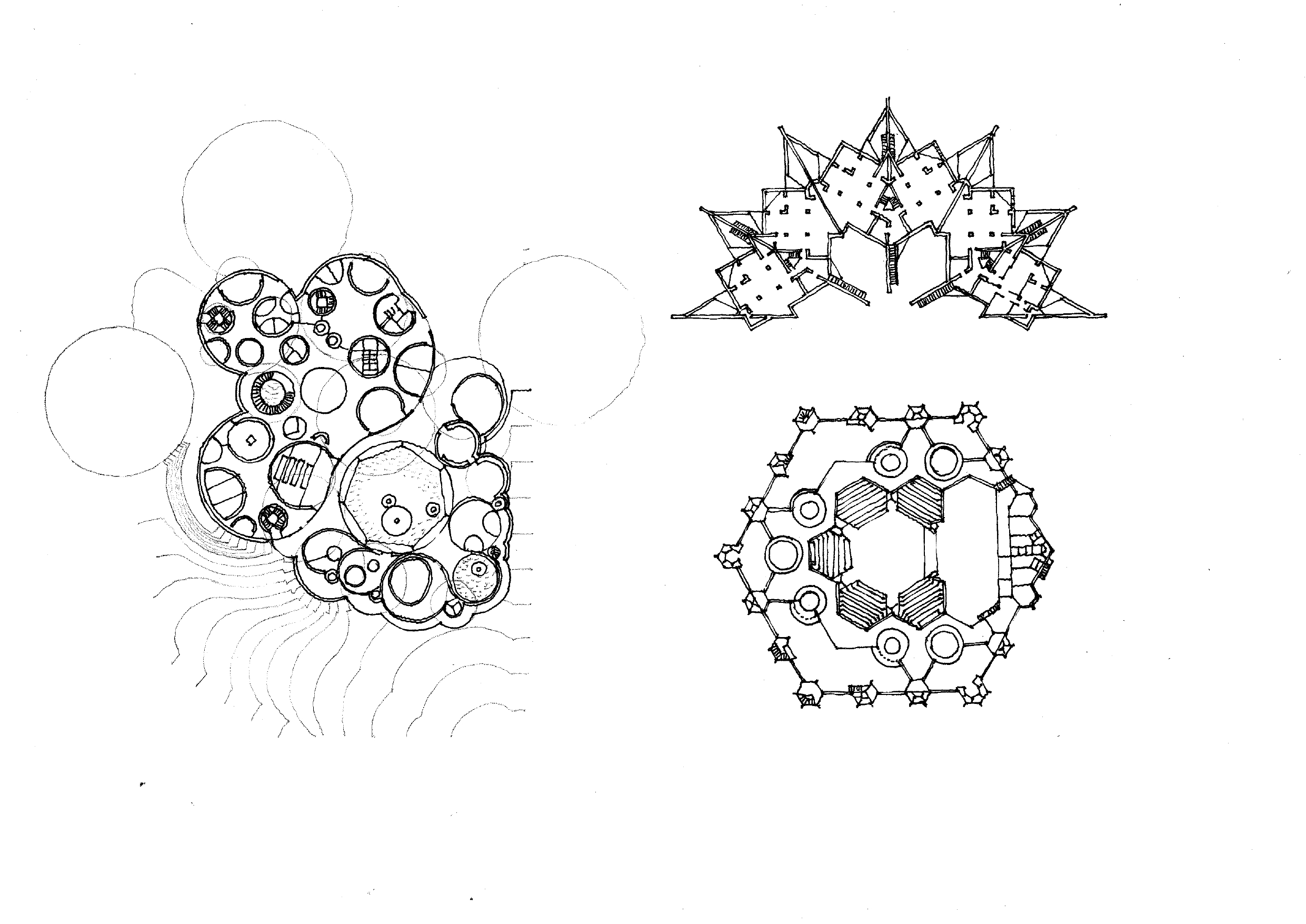
Balra: Mansilla y Tuñon: Városháza, Lalin, 2011; jobbra fent: Zvi Hecker: Ramot Housing II. ütem, Jeruzsálem, 1979–1983; jobbra lent: Piet Blom: Színház és kulturális központ, Helmond, 1964–1967

A matematikai modellek között jellegzetes mintázatot képeznek a véletlen statisztikailag leképezett formációi, amelyek szintén az építészek figyelmének középpontjába kerültek. Sou Fujimoto óvodaépületének (Children’s Center for Psychiatric Rehabilitation, Japán) alaprajzi egységei a dobókockák spontán elrendeződését mutatják, de az elemek térkapcsolataiban a hagyományos buddhista építészet sarkokon egymásba kapcsolódó helyiségeire is utalnak. A marokkójáték véletlenszerűen egymáson elhelyezkedő pálcikáira emlékeztet a Herzog & de Meuron építésziroda 2010-ben felépült irodaház-együttese (Actelion Business Center, Allschwil). Szintén a véletlen generálásán alapulnak a hálózatok jellegzetes formációit megvalósító épületkísérletek. Daniel Libeskind berlini Zsidó Múzeumának alaprajzi formáját egy két háború közti berlini telefonkönyvből kiválasztott címek térképen lévő pontjainak összekötésével szerkesztették. Az alaprajzi forma alapján asszociálhatunk az összetört Dávid csillagra, vagy az SS-jelvény villámformájára is.
És ha már a véletlen formációiról beszélünk, a káoszelmélet jellegzetes mintázatait is említenünk kell, a fraktálok képeit mint a tudományok által feltárt jellemző mintázatokat. A nyolcvanas évek egyik érdekes kísérlete volt Zwi Hecker berlini iskolája, a Heinz Galinsky Schule, amelynek centripetális alaprajzi rendszere a fraktálokat idézi. A kortárs építészetben a TEd’A Arquitectes építésziroda felvállalt térképzési filozófiája hasonló elveket követ. Can Miquel-i na Catiban épült villaépületük centrálisan szimmetrikus alaprajzot követ, de a főhelyiségekhez kapcsolódó kiszolgáló helyiségcsoportok fraktálszerűen szerkesztettek.

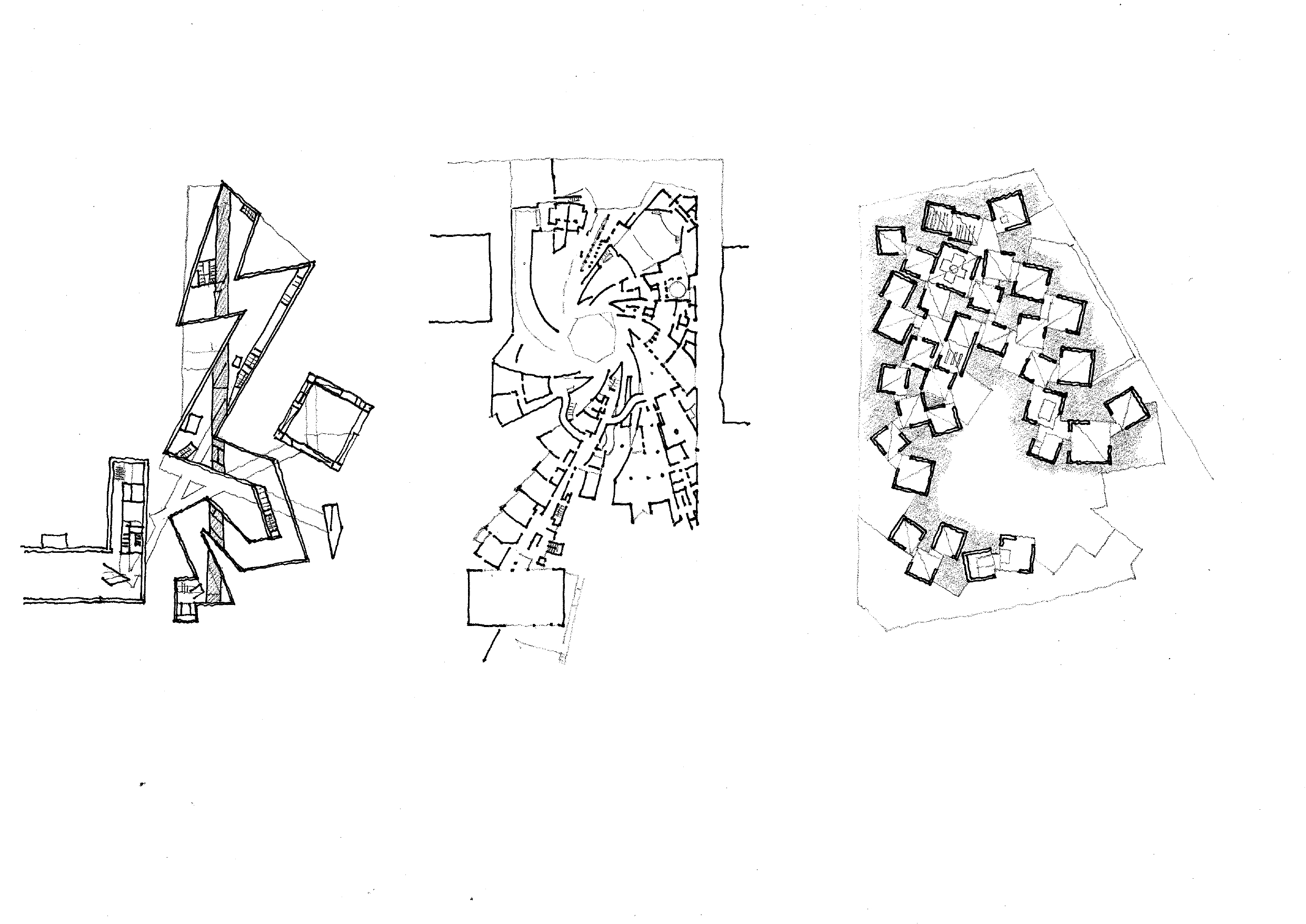
Balra: Daniel Libeskind: Zsidó Múzeum, Berlin, 1999; középen: Zvi Hecker: Heinz Galinsky Schule, Berlin, 1992–1995; jobbra: Mansilla y Tuñon: Vega Baja Museum terve, Toledó, 2010

Formációk: anti-utópiák, vernakuláris mintázatok, a történeti városok képződményei

Az előzőekben tárgyalt történeti és kortárs alaprajzi és térkísérletek jellemezhetők egyfajta utópikus jelleggel. (Végül is minden olyan térbeli konstrukció, amely valamilyen elvont/absztrakt formációt valósít meg, ab ovo utópikus – még ha ezt az utópiát „telekhatárokon belül” is próbálják megvalósítani). És itt fontos szerepet játszik a hagyományos ornamentika, a díszítőművészet, amely az elvont térbeli formációkat „tovább magyarázza”, narratívákkal látja el, és ezáltal „humanizálja”.16
A 20. század közepén megindult etnográfiai és antropológiai kutatások által feltárt „kvázi-antiutópikus” településformációk ebben a tekintetben is új dimenziókat nyitottak. Lévi-Strauss kutatásai nyomán az építészek egy jelentős csoportja a vernakuláris mintázatok felé fordult. A holland strukturalisták csoportját ilyen irányú érdeklődésük miatt „antropozófus építészeknek” nevezték. Megindult az észak-afrikai és távol-keleti kultúrák archetipikus formációinak kutatása. Az egyik legtöbbet forgatott könyv lett Bernard Rudofsky Architecture without Architects című opusza, amelyben az ősi civilizációk épületeinek képei követendő mintákként szolgáltak – és szolgálnak ma is. Herman Hertzberger és Aldo van Eyck a dogon és a kasbah törzsi települési struktúrák tanulmányozása alapján, azok geometrikus stilizálásával tervezték a Central Beheer biztosító és az amszterdami árvaház épületeit.
Az anonim, spontán történeti építészet vizsgálata, a spontán várostranszformáció mintázatai is a nagy szerkesztett-épített struktúrák – a megépült utópiák – ellenében hatnak; ez a fajta építés is mintává vált. A történeti városok, a népi építészet, vagy éppen a természet spontán formációit idézik a szerves, kontextuális beépülés, igazodás mintázatai Alvar Aalto és mások organikus formációiban, Álvaro Siza, Enric Miralles „szabálytalan szerkesztéseiben”. A Mansilla + Tuñón iroda érdekes próbálkozása a toledói pályázatuk (Vega Baja Museum pályázati terve), ahol egy meglévő spontán történeti képződmény struktúráját adaptálják egy újonnan tervezett beépítésre.
A tervezés folyamatában előbb-utóbb szerkeszteni kezdünk, és szerkesztési módszereinket meghatározzák geometriai tudásunk és végső soron a világról alkotott képzeteink. Legalábbis azok az építészek, akik épületeiket nem pusztán a funkció kielégítésének tekintik, olyan alaprajzi-térbeli mintázatokat valósítanak meg, amelyek a világban felismert általánosabb igazságokra, tendenciákra reflektálnak. Ehhez leginkább a (természet)tudományok tárhatnak elénk olyan absztrakt, vagy szemléletes formációkat, amelyek bővítik, megváltoztatják a világról alkotott képzeteinket.
A 20. századi és a kortárs épületek alaprajzi mintázatai sokfelé szétágaznak, de az igény a strukturális szerkesztettségre, a koherens térszervezésre tovább él az újabb fajta mintázatok (fraktálok, hálózatok, biomorf formációk) alkalmazása során is. Mindeközben a hagyományos ornamentika és a szimmetriarendszerekre épülő szerkesztések is érvényesek és kombinálódnak az újabb formációkkal. Az ornamentika geometrikus szerkesztő módszereinek kutatása, a szerkesztések akár manuális, akár digitális technikán alapuló elemzése és tanítása több haszonnal is kecsegtethet. Egy jól használható szerkesztési módszert adhat az építész hallgatók kezébe, strukturális gondolkodásra taníthatja őket, megértetheti velük az építészettörténet tanulmányozása során látott alaprajzi és térbeli rendszerek összefüggéseit, továbbá ösztönzést adhat arra, hogy a modern és kortárs építészet alkotásait ne csak másolható képekként kezeljék, hanem elemezhető és elemzendő struktúrákként.

(Magyar Építőművészet Utóirat 2024/5)

Jegyzetek

1 Az alaprajzokban megnyilvánuló strukturális rend pedig a térszervezés és térképzés lenyomata.
2 Szentkirályi Zoltán: A barokk forma objektivitásáról. Építés- és Közlekedéstudományi Közlemények, 1963. 1-2. Különnyomat
3 Utalva Nietzsche fogalomhasználatára, a tektonikus mintázatokat dionüszoszinak, az atektonikusakat apollóninak tekintem. Míg az előző az anyag valóságához kötődő, „földi”, az utóbbi elvont, szellemi, „égi” tulajdonságokkal bír. Lásd Friedrich Nietzsche: Ifjúkori filozófiai írások. Európa Kiadó, Budapest, 1988. A dionüszoszi-apollóni kettősséghez lásd még Szent-Györgyi Albert írását Dionüszosz és Apolló követői a kutatásban címmel: https://www.ponticulus.hu/rovatok/hidverok/dionuszosz.html#gsc.tab=0
4 Antoine Picon: Ornament – The Politics of Architecture and Subjectivity. John Wiley & Sons Ltd, 2013. Az állítás meglehetősen sarkított és vitatható, mert az építészetben a téralkotás-téralakítás fontossága megkérdőjelezhetetlen.
5 Owen Jones: The Grammar of Ornament. Day & Son (Lincoln’s inn Fields, London, 1856), magyarul: Ornamentika. Népek, korok díszítőelemei. Cser Kiadó, Budapest, 2004
6 Katona Júlia: A díszítő elme és a díszítő kéz. Ornamentikairodalom a 20. században, valamint ugyanő: Az ornamens csontváza – Lewis F. Day tervezéselmélete. Műértő, 2005 december
7 Ennek a tulajdonképpen parametrikus eljárásnak (illetve Owen Jones-nál ennek a visszafordításáról van szó) a kortárs építészetben van igazán nagy jelentősége, mert a digitális képalkotó-szerkesztő eljárások bármely (parametrikus, torzított stb.) felületen képesek mintázatokat megjeleníteni (absztrakt ábrákat vagy képeket), készüljenek ezek bármilyen anyagból.
8 lásd a 6. számú lábjegyzetet
9 Az ornamensek ismétlésével szerkesztett mintázatoknak a bőség reprezentálása mellett, eredetét tekintve – az áldozatos kézzel végzett munkára gondolva – szakrális funkciója is van.
10 A 20. század elején Huszka József, aki a magyar népi ornamentika motívumkincseit gyűjtötte, középiskolásoknak írt geometria tankönyvében a geometriai szerkesztéseket ornamensek rajzolásával illusztrálta-tanította. Ez is azt példázza, hogy korábban a geometriát nem csak elvont törvényeket és szabályokat taglaló diszciplínaként, hanem gyakorlati célokra alkalmazva oktatták. Lásd Katona Júlia idézett tanulmányait.
11 Nem vizsgálva most a 18. századtól az angol romantikus építészettel megjelenő aszimmetrikus formációkat, vagy például a buddhista, taoista építészet nem szimmetriára épülő szerkesztéseit.
12 Ezeknek az izometrikus transzformációknak jól áttekinthető és frappáns ábrákkal történő megjelenítéseit láthatjuk pl. Lionel March és Philip Steadman: Geometria az építészetben című könyvében, Műszaki Könyvkiadó, Budapest, 1973
13 Hargittai Magdolna – Hargittai István: Képes szimmetria. Galenus Kiadó, 2005
14 Technikailag a motívumok másolhatósága és sokszorozhatósága érdekében szükség van a szerkeszthetőségre.
15 A geometria alapelemei egyúttal a legősibb szimbólumok is. Például a kör a teljességet, a világmindenséget, az égboltozatot, az égit (istenit) szimbolizálja, a négyzet vagy téglalap a házat, a földet az anyagi dolgokat jelentette, a háromszög a tökéletességet, a kiegyensúlyozottságot, a Szentháromságot stb.
16 Ezzel kapcsolatban figyelemre méltó Földényi F. László írása, amely az elvont térrendszerek esetében felveti az „embertelenség” dimenzióját. Földényi F. László: Az eleven halál terei – Kafka, de Chirico és a többiek. Jelenkor Kiadó, 2018